

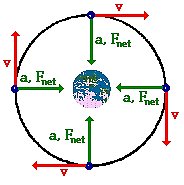
An orbiting planet is in fact a freely falling body.Įquation ( 42) is a special case (for circular orbits) of Kepler’s third law, which is discussed in the article celestial mechanics. This occurs for exactly the same reason that all bodies fall toward Earth with the same acceleration and that the period of a pendulum is independent of its mass. It should be noted that the speed does not depend on the mass of the planet. Combining these equations yields a relation between the speed v of a planet and its distance r from the Sun: The earthbound observer then believes that there is no net force acting on the planet-i.e., that F + f = 0, where F is the force of gravity given by equation ( 41). The pseudoforce f needed to balance this acceleration is just equal to the mass of Earth times an equal and opposite acceleration, or f = M E v 2/ r. In the case of orbital motion, the outward pseudoforce that balances gravity is called the centrifugal force.įor a uniform circular orbit, gravity produces an inward acceleration given by equation ( 40), a = − v 2/ r. The apparent force, known in mechanics as a pseudoforce, is due to the fact that the observer is actually in accelerated motion. Earth is in freely accelerated motion caused by an unbalanced force. In other words, if gravity is trying to pull Earth into the Sun, some opposing force must be present to prevent that from happening. It would appear to the observer, therefore, that any force (such as the Sun’s gravity) acting on Earth must be balanced by an equal and opposite force that keeps Earth in equilibrium. To an observer on the surface of Earth, the planet appears to be at rest at (approximately) a constant distance from the Sun. The force acts along the direction connecting the two bodies (i.e., along the radius vector of the uniform circular motion), and the minus sign signifies that the force is attractive, acting to pull Earth toward the Sun. The gravitational force between two bodies such as the Sun and Earth is given by where M S and M E are the masses of the Sun and Earth, respectively, r is the distance between their centres, and G is a universal constant equal to 6.674 × 10 −11 Nm 2/kg 2 (Newton metres squared per kilogram squared). The force of gravity serves to overcome the inertial tendency of the planet, thereby keeping it in orbit. In the absence of gravity, the planet would obey the law of inertia (Newton’s first law) and fly off in a straight line in the direction of the velocity at constant speed. The reason is that, at each instant, the velocity of the planet is tangent to the orbit.
#Circular orbit how to
COVID-19 Portal While this global health crisis continues to evolve, it can be useful to look to past pandemics to better understand how to respond today.Student Portal Britannica is the ultimate student resource for key school subjects like history, government, literature, and more.This Time in History In these videos, find out what happened this month (or any month!) in history.#WTFact Videos In #WTFact Britannica shares some of the most bizarre facts we can find.Demystified Videos In Demystified, Britannica has all the answers to your burning questions.Britannica Explains In these videos, Britannica explains a variety of topics and answers frequently asked questions.
Britannica Classics Check out these retro videos from Encyclopedia Britannica’s archives.


 0 kommentar(er)
0 kommentar(er)
